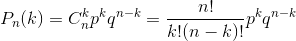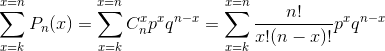Неожиданное для меня самого продолжение истории с изучением механик с использованием игровых кубиков. В настольной игре “Ужас Аркхэма” наткнулся на любопытную механику проверок, захотелось посмотреть вероятности того или иного исхода, что и вылилось в небольшое исследование, результатами которого хочу здесь поделиться.
Проверки
Со времен первых настольных ролевых игр появилась механика проверок (check), которая применялась для определения успешности тех или иных действий игрового персонажа.
Пример:
У нас некоторый персонаж, перед которым стоит задача выломать дверь. Чтобы определить получиться ли у него выполнить эту задачу или нет, задается некоторая условная сложность задания, допустим — 10. Так же у персонажа есть условный цифровой показатель его физической силы, например 6. Мы задаем условия успешного выполнения задачи: если сумма показателя физической силы и результата броска кубика (d6) будет равна или превысит сложность задачи, то задача выполнена успешно. В противном случае нас ждет провал.
Получается, что в данном примере при сложности задачи 10 и силе персонажа 6, для успеха необходимо выбросить на кубике значение 4 и выше (4+). Т.е. вероятность успеха 50%.
Персонажу с силой 4 удастся решить задачу только при значении 6 на кубике.
С силой 10 даже не придется браться за кубик, ровно как и с силой 2. В обоих случаях исход проверки известен сразу.
Таким образом механика проверок связывала значение условного параметра персонажа с шансами выполнить этим персонажем какие-либо действия. В том числе сюда включались различные проверки на внимательность (заметил ли персонаж ловушку в стене), реакцию (смог ли увернуться от брошенного в него камня), устойчивость к воздействиям (опьянел ли с первой кружки добротного грога) и тому подобное.
Вариантов механик осуществляющих проверку существует множество. Здесь же мы рассмотрим одну из них, примененную в игре “Ужас Аркхэма”. Подозреваю, что создатели игры позаимствовали эту механику у кого-то, но автора этой механики мне пока обнаружить не удалось.
Механика
В игре “Ужас Аркхэма” используется следующая механика проверки:
Навык персонажа определяет количество бросков дайса d6.
Сложность задачи определяет количеством бросков, которые должны быть “успешными”.
Успешным броском считается бросок при котором на кубике выпадет значение 5 или 6.
Пример:
Персонаж встретился со страшным монстром, нужно узнать испугался ли наш персонаж этого монстра или нет. Толщина нервов и невозмутимость определяются в игре параметром “Воля”. Для примера допустим что “воля” нашего персонажа имеет значение 4. Монстр настолько страшен, что для успешной проверки необходимо 2 успешных броска. Это значит, что для успешного прохождения проверки, 2 из 4 брошенных кубиков должны показать 5 или 6.
Если бы значение “Воли” было 1, то кидать кубики не пришлось бы, поскольку броском 1 кубика явно не получить 2 успешных 🙂
Однако, сколь бы высокое значение “Воли” мы не имели, кидать кубики все равно придется, поскольку шанс при котором ни один кубик не покажет 5 или 6 сохраняется всегда.
Меня заинтересовала данная механика и я решил посчитать вероятности успешного прохождения проверок при различных сочетаниях количества бросков и требуемого успеха. Причем любопытно стало найти универсальное решение для любого количества бросков, требуемых проверок, вариантов дайса и условий успешного броска.
Если вас интересует результат, то его можно увидеть здесь. Пользуйтесь на здоровье 🙂
Далее же будет описание процесса, которое будет интересно начинающим математикам и любителям теории вероятностей 🙂
Вероятность “успеха” для 1 броска
Вероятность успеха для одного броска определяется весьма просто. Достаточно разделить количество граней, означающих успешный бросок, на общее количество граней.
Для простоты все наши изыскания будем проводить на примере классического игрового кубика d6.
Если успех означает бросок с результатом 5 или 6, то вероятность такого успеха для одного кубика:
2/6 = ⅓ = 33%
Соответственно, вероятность провала:
4/6 = ⅔ = 66%
Введем два обозначения: p и q
В дальнейшем повествовании будем считать, что p — это вероятность успешного броска. A q — вероятность провала.
С этого момента для нас, по большому счету, уже не имеет значение какое количество граней у бросаемого нами дайса и при каких условиях засчитывается успешный бросок.
Нас интересуют только 2 значения: вероятность успеха и провала для одного броска, которые к тому же тесно связаны друг с другом:
p = 1-q
q = 1-p
Для справки, значения p и q для d6:
| Успех | 1+ | 2+ | 3+ | 4+ | 5+ | 6+ |
|---|---|---|---|---|---|---|
| p | 100% | 83,33% | 66,67% | 50% | 33,33% | 16,67% |
| q | 0% | 16,67% | 33,33% | 50% | 66,67% | 83,33% |
Вероятность успеха для 2 бросков
С двумя бросками все немного интересней.
Если нужно определить вероятность успешности обоих бросков, то можно воспользоваться тем же методом, что и в предыдущей статье.
Достаточно перемножить между собой вероятности успеха:
p*p
Для примера мы всегда будем рассматривать d6 и успех при 5+, т.е. p = 1/3 а q=2/3
p*p = 1/3*1/3 = 1/9 = 11,11%
Соответственно вероятность “провала” для обоих кубиков:
q*q = 1/3*2/3 = 4/9 = 44,44%
Существует еще вероятность того, что один кубик покажет “успех”, а другой “провал”. И такая вероятность равна:
p*q = ⅓ * ⅔ = 2/9 = 22,22%
Однако, если мы теперь просуммируем вероятности, то увидим:
p*p + q*q + p*q = 1/9 + 4/9 + 2/9 = 7/9
что сумма вероятностей не сходиться к 1. Т.е. мы не учли всех возможных вариантов исхода броска двух кубиков.
Оказывается, рассматривая вероятность события когда один кубик покажет “успех”, а другой “провал”, мы учли только тот вариант, при котором первый кубик покажет успех, а второй — провал. Событие, при котором все будет наоборот (первый кубик — “провал”, а второй — “успех”) необходимо учитывать отдельно:
q*p = p*q = 2/9
И тогда мы получим полный перечень всех возможных исходов для броска двух кубиков:
p*p + q*q + p*q + q*p = 1
Введем еще одно обозначение:
Pn(k) — это вероятность пройти проверку, в которой из n бросков k должны быть успешными.
Это именно та величина, которая интересует нас во всех случаях.
Для n=k=1 при p = 1/3 все просто, P1(1) = 1/3 = 33,33%
Для n=k=2 при p=1/3, тоже: P2(2) = p*p = 1/9 = 11,11%
А вот если нас интересует ситуация когда из двух бросков нам достаточно одного успешного, то нас устраивают сразу 3 исхода из 4 возможных: p*p, p*q и q*p
То есть для n=2 и k=1 при p=1/3 , P2(1) = p*p + p*q + q*p = 1 — q*q = 5/9 = 55,56%
Вероятность успеха для 3 бросков
А что произойдет, если мы будем бросать 3 кубика?
Возможны следующие события:
- Ни один кубик не покажет “успеха” — qqq
- Все кубики покажут успех — ppp
- Один кубик покажет “успех” — pqq
- Два кубика покажут “успех” — ppq
Причем два последних события существуют в 3 вариантах каждое:
- pqq, qpq, qqp
- ppq, pqp, qpp
Получается, что:
P3(3) = ppp
P3(2) = ppp+ppq+pqp+qpp = ppp+ppq*3
P3(1) = ppp+ppq+pqp+qpp+pqq+qpq+qqp = ppp+ppq*3+pqq*3
Однако мы же ставили перед собой задачу найти общую формулу для вычисления Pn(k) для любых n, k, p и q. А не считать каждый раз количество исходов, которое к тому же будет возрастать в прогрессии.
Формула для Pn(k), при n=k достаточно очевидна:
Pn(n)= p^n
Так же очевидна формула при k=0:
Pn(0) = q^n
Все вопросы возникают когда 0
Для начала упростим себе подсчет количества вариантов выпадения схожего события, обозначим это число как C(n,k), где n — количество бросков, а k — количество успешных бросков. Подсчитать такую комбинаторику помогают факториалы:
C(n,k) = n! / k! (n-k)!
Вероятность наступления одного варианта данного события, равна:
p^k * q^(n-k)
В совокупности получаем:
А если быть точнее, то формулу, которая уже более 300 лет известна как формула Бернулли, что дает нам право поздравить себя с очередным изобретением велосипеда 🙂
Отлично, найти вероятность того, что из n бросков k будут успешными мы можем по формуле замечательного швейцарского математика. Однако нас интересует вероятность того, что k и более бросков будут успешными, а не только k. А для этого нам всего лишь нужно просуммировать вероятности Pn(x), где x принимает значения от k до n:
Собственно, данная формула и есть цель наших изысканий 🙂
Результаты изысканий
Найдя необходимую мне формулу и в очередной раз проникшись уважением к Якобу Бернулли, я сделал электронную таблицу, которая позволяет рассчитать вероятности успешного прохождения проверки для любого количества бросков любых вариаций дайсов. Таблицу выложил в открытый доступ всем желающим. Пользуйтесь на здоровье 🙂